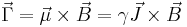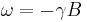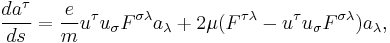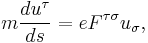Larmor precession
In physics, Larmor precession (named after Joseph Larmor) is the precession of the magnetic moments of electrons, atomic nuclei, and atoms about an external magnetic field. The magnetic field exerts a torque on the magnetic moment,
where 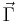 is the torque,
is the torque,  is the magnetic dipole moment,
is the magnetic dipole moment, 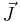 is the angular momentum vector,
is the angular momentum vector, 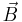 is the external magnetic field,
is the external magnetic field, 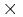 symbolizes the cross product, and
symbolizes the cross product, and 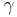 is the gyromagnetic ratio which gives the proportionality constant between the magnetic moment and the angular momentum.
is the gyromagnetic ratio which gives the proportionality constant between the magnetic moment and the angular momentum.
Contents |
Larmor frequency
The angular momentum vector 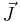 precesses about the external field axis with an angular frequency known as the Larmor frequency,
precesses about the external field axis with an angular frequency known as the Larmor frequency,
where  is the angular frequency,[1]
is the angular frequency,[1] 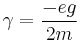 is the gyromagnetic ratio, and
is the gyromagnetic ratio, and  is the magnitude of the magnetic field[2] and
is the magnitude of the magnetic field[2] and  is the g-factor (normally 1, except for in quantum physics).
is the g-factor (normally 1, except for in quantum physics).
Simplified, this becomes:
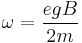
where  is the Larmor frequency, m is mass, e is charge, and B is applied field.
is the Larmor frequency, m is mass, e is charge, and B is applied field.
Each isotope has a unique Larmor frequency for NMR spectroscopy, which is tabulated here.
Bargmann-Michel-Telegdi equation
The spin precession of an electron in an external electromagnetic field is described by the Bargmann-Michel-Telegdi (BMT) equation [3]
where 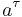 ,
,  ,
,  , and
, and  are polarization four-vector, charge, mass, and magnetic moment,
are polarization four-vector, charge, mass, and magnetic moment, 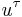 is four-velocity of electron,
is four-velocity of electron, 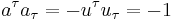 ,
, 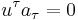 , and
, and 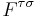 is electromagnetic field-strength tensor. Using equations of motion,
is electromagnetic field-strength tensor. Using equations of motion,
one can rewrite the first term in the right side of the BMT equation as 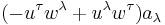 , where
, where 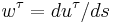 is four-acceleration. This term describes Fermi-Walker transport and leads to Thomas precession. The second term is associated with Larmor precession.
is four-acceleration. This term describes Fermi-Walker transport and leads to Thomas precession. The second term is associated with Larmor precession.
Applications
A 1935 paper published by Lev Landau and Evgeny Lifshitz predicted the existence of ferromagnetic resonance of the Larmor precession, which was independently verified in experiments by J. H. E. Griffiths (UK) and E. K. Zavoiskij (USSR) in 1946.
Larmor precession is important in nuclear magnetic resonance, electron paramagnetic resonance and muon spin resonance.
To calculate the spin of a particle in a magnetic field, one must also take into account Thomas precession.
See also
Notes
- ^ Spin Dynamics, Malcolm H. Levitt, Wiley, 2001
- ^ Louis N. Hand and Janet D. Finch. (1998). Analytical mechanics. Cambridge, England: Cambridge University Press. p. 192. ISBN 9780521575720. http://books.google.com/?id=1J2hzvX2Xh8C&pg=PA192&lpg=PA192&dq=Larmor's+Theorem.
- ^ V. Bargmann, L. Michel, and V. L. Telegdi, Precession of the Polarization of Particles Moving in a Homogeneous Electromagnetic Field, Phys. Rev. Lett. 2, 435 (1959).